Prove that Vertex Cover is NP-hard problem

Question

Vertex Cover problem is defined as follows:

Given a Graph G and integer k.

Does G have a subset S of vertices, such that: |S| = k, and every edge in G has at least one of the end points in S.

Prove that Vertex Cover is an NP-hard problem by showing a reduction from one of the known NP-complete problems.

Answer 1

Because in a graph G, if we are given a vertex cover, we can find the remaining set of vertices to be a set of independent set. Thus we can do the following reduction in polynomial time:

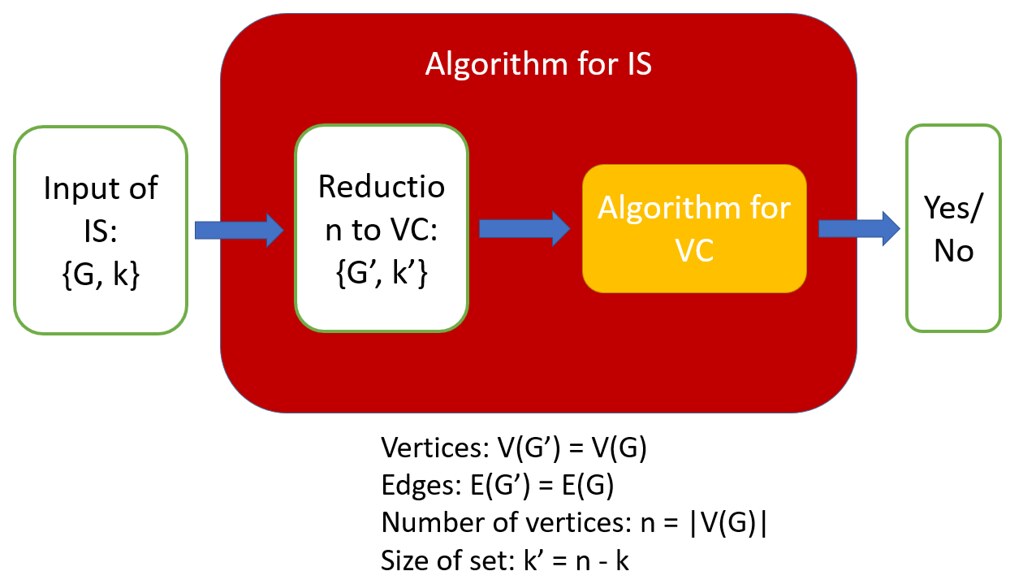
That means, if we want to find the minimum VC, we can do so by finding out the maximum  IS.

As IS is proven to be NP-hard, VC is NP-hard too.

The full chain starting SAT can be written as:

SAT <=p CLIQUE <=p Independent Set <=p Vertex Cover