k-degree constrained spanning tree

Question

Finding a spanning tree is an easily solvable polynomial time problem. Consider a "k-degree constrained spanning tree", wherein we have to find a spanning tree such that no vertex in the spanning tree has degree more than k.  Show that k-degree constrained spanning tree problem is NP-complete.

Answer 1

NP complete proof:

To prove that a problem is NP-complete, we must show that it is in NP and that it is NP-hard.

1. For the "k-degree constrained spanning tree" problem, given a spanning tree, we can easily check in polynomial time whether it covers all vertices in the graph (which makes it a spanning tree) and whether each vertex in the tree has a degree of no more than k. This verification process involves checking each vertex and its edges, which can be done in polynomial time relative to the size of the graph.

2. Selected Hamiltonian path problem to show the reduction from Hamiltonian path to k-degree constrained spanning tree. Hamiltonian path problem is a known NP - complete problem.

3. Reduction from Hamiltonian Path to k-Degree Constrained Spanning Tree

i.)Start with a graph G for the Hamiltonian Path problem.

ii.)Transform G into a new graph G' for the k-degree constrained spanning tree problem. We do this by adding a new vertex Vnew​ to G and connecting Vnew​ to every other vertex in G

iii)Set k = 2 for the spanning tree problem in G'. 

The idea is that if there is a Spanning tree in G' with degree 2 constrained (including Vnew) then the spanning tree is the Hamiltonian path in graph G after removing Vnew.

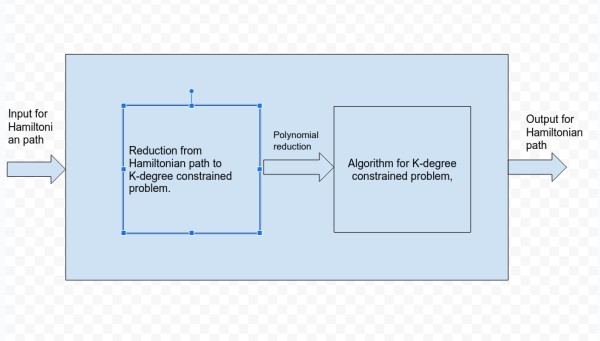
So, Hamiltonian path problem is polynomial time reducible to k-degree constrained spanning tree.

We know that Hamiltonian path problem is NP complete problem so k-degree constrained spanning tree problem is atleast hard as Hamiltonian path problem.

So k-degree constrained spanning tree problem is NP - Complete.

Answer 2

If in a tree, the maximum degree is 2 , then the tree is simply a path. This allows us to observe that the problem of finding spanning tree where no vertex has degree more than 2 is equivalent to finding a Hamiltonian path.

Therefore, the k -degree constrained spanning tree problem is simply a generalization of the Hamiltonian Path problem. Specifically, Hamiltonian Path problem can be directly reduced to the k -degree constrained spanning tree problem by leaving the original graph unchanged and simply using the value of k = 2 .