“Discovery of the Sun”

Question

A "sun" graph looks like a circle, with a hanging vertex on the each vertex on the loop.  The problem to discover the sun is defined as follows: Given a graph G, identify, is there a sun graph inside the given graph G?

Prove that this problem is NP-complete using any of the known NP-complete problems as a starting point.

Answer 1

Other than the vertices on the periphery of the sun, the cycle is a Hamiltonian cycle on the remaining vertices.

This observation allows us to reduce the Hamiltonian Cycle problem to the Discovery of the Sun problem in the following manner.

Given a graph G with n vertices, we construct a new graph G’ by adding n new vertices and connect each new vertex a corresponding old vertex. Clearly, G has a Hamiltonian cycle if and only if G’ has a sun graph inside that spans all the vertices of G’.

Answer 2

This problem can be reduced into multiple other NP-Complete problems such as clique, vertex cover and hamiltonian cycle to my knowledge.
For Sun Graph to Hamiltonian Cycle Reduction: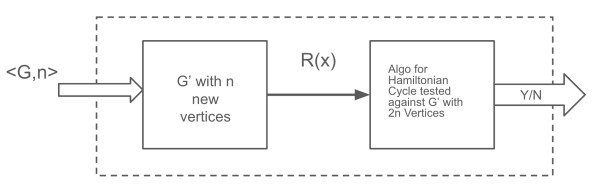

Consider R(x)= Connects each new vertex added to corresponding vertex in Original graph G

From the above figure,

• If G possesses a Hamiltonian cycle, we can construct a sun graph in G' by:
  • Adding the hanging vertices to the cycle.
  • Connecting each hanging vertex to a new vertex outside the cycle
• Conversely, removing the hanging vertices from a sun graph in G' reveals a Hamiltonian cycle in the original graph G.

From this reduction we can say that solving the Sun Graph problem requires tackling a problem as hard as Hamiltonian Cycle. So, the Sun Graph problem must also be NP-complete, due to its inherent complexity.

For Sun Graph to Clique:

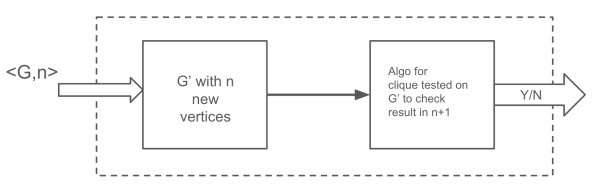
G to G':

• Add n new vertices to G. 
• Connect each new vertex to its corresponding vertex in G. 
• Add an additional edge between every pair of new vertices in G'. 
• Additionally, for each pair of hanging vertices, add an edge connecting them.

Explanation for above figure(Clique):

• If G has a sun graph, we can construct a clique of size n + 1 in G' as follows:

  • Include all n hanging vertices in the clique. Select one vertex from each pair of connected new vertices and add it to the clique.

• Conversely, if G' has a clique of size n + 1, we can construct a sun graph in G as follows:

  • Remove the edges between new vertices. The remaining edges form a sun graph in G, with the hanging vertices connected to the selected vertex from each pair of connected new vertices.

From this reduction we can say that solving the Sun Graph problem requires tackling a problem as hard as Clique . So, the Sun Graph problem must also be NP-complete, due to its inherent complexity.